Конструкция и расчет роторного вагоноопрокидывателя

Роторный вагоноопрокидыватель может быть передвижным или стационарным.

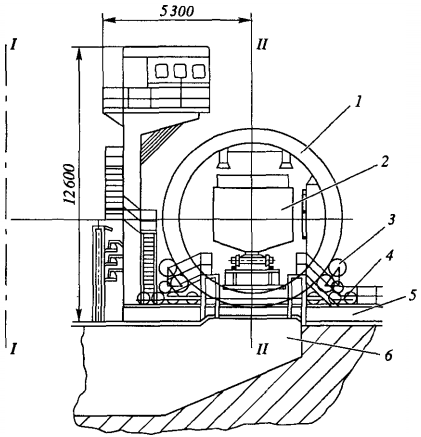
Передвижной роторный вагоноопрокидыватель (рисунок  1) выполнен в виде круговой роторной металлоконструкции, ободы которой устанавливаются на скатах 3,  закрепленных на мосту 4.  Мост устанавливается на ряд тележек, перемещающихся по рельсам 5. В одном положении (І-І) вагон заталкивается толкателем в ротор. В другом (ІІ-ІІ) ротор 1 поворачивает вагон, предварительно закрепленный, на 180° для разгрузки шихты в траншею или бункер 6. В отличие от передвижного ротора у стационарного опоры роликовых скатов закреплены прямо над бункерами.

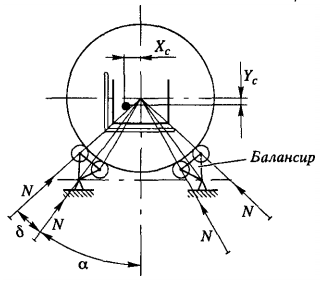
Расчетная схема механизма кантования приведена на рисунки 2.

Общий момент сопротивления при кантовании ротора М = М₁ + М₂. Момент сопротивления М₁ от веса люльки G_л и вагонов G_в:

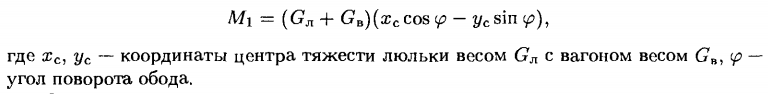
Момент трения:

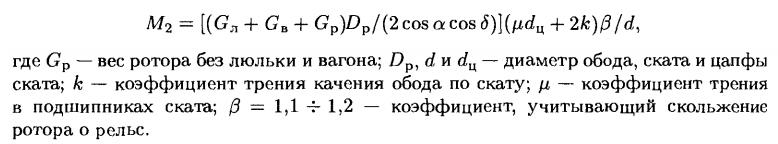
Статический момент на валу электродвигателя определяется передаточным отношением i от двигателя к зубчатке ротора и равно М_с= М/(iη). Дальнейший расчет механизма кантования проводится аналогично выбору и проверке двигателей для башенного вагоноопрокидывателя.

Одним из наиболее нагруженных узлов роторного вагоноопрокидывателя является его обод (или бандаж). На рисунки 3 приведена расчетная схема прочности обода.

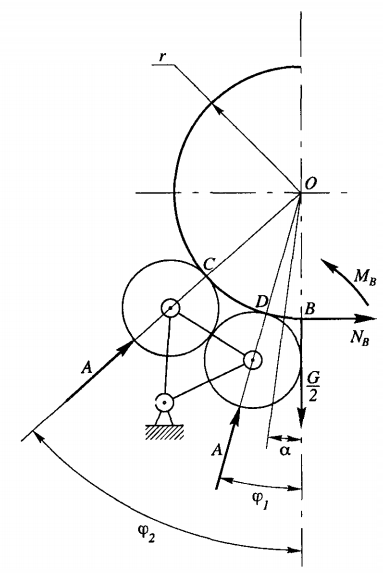
Условно будем считать нагрузку G, приходящуюся от веса ротора, вагона с шихтой, симметричной относительно центра О и приложенной к ободу в точке В. В сечении В действует горизонтальная сила N_в, перерезывающая сила Q = G/2 и момент М_в. Здесь G — нагрузка на один обод опрокидывателя. Для любого текущего угла α ≤ φ₁ между параметрами устанавливаются следующие связи:

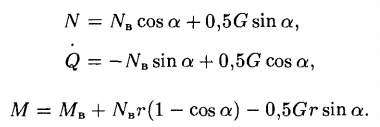
В интервале углов φ₁ ≤ α ≤ φ₂ связи будут другими:

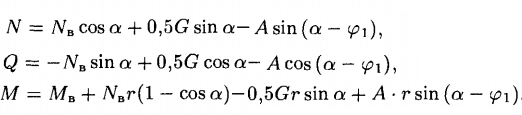
Наконец, для диапазона φ₂ ≤ α ≤ π/2

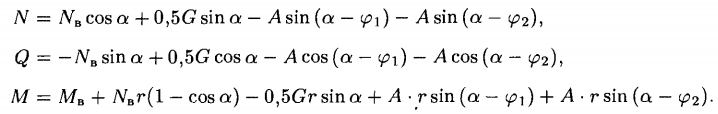
Для стандартных величин φ₁ = 20° и φ₂ = 40° соотношение 2А(cos40° + + cos20°)=G и реакция A = 0,293G.

Неизвестные параметры N_в и М_в определим из условий, что в точках С и D прогибы у_в = y_D =0

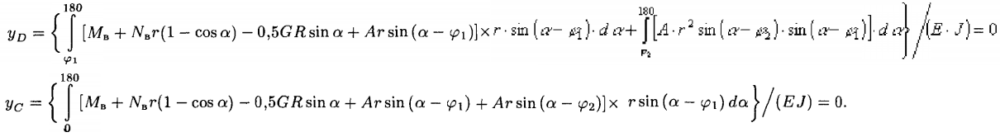
Решением этих уравнений будет N_в = —0,151 G и Мв = 0,117 Gr. По этим данным вычисляются относительные перерезывающая Q=Q/b, нормальная N = N/b и моментная M=M/(Gr) нагрузка (таблица 1).

Максимальные напряжения в любом сечении обода

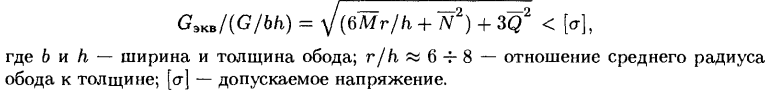
В таблице 1 приведено распределение напряжений по сечениям. Из результатов видно, что наибольшее напряжение будет под удаленным скатом (φ₂ = 40°):